Sabias algo acerca de los números primos

¿Sabías algo acerca de los números primos?

De los números primos se han establecido: el Teorema Fundamental de la Aritmética, el Lema de Euclides, el Pequeño Teorema de Fermat, el Teorema de Wilson, el Postulado de Bertrand, el Teorema de Dirischlet... También se han distinguido algunas clases de ellos: los de Fermat, los de Mersene, los de Sophie Germain y los números primos llamados gemelos. Además se han propuesto conjeturas como la de Goldbach, o la de que existen infinitos pares de números primos gemelos.

El trabajo mostrado en este sitio pretende ofrecer una aportación al tema de la lógica de aparición de los números primos, que parecía irresoluble. Se trata de demostrar que los números primos no aparecen al azar entre los números naturales, sino que guardan una secuencia de aparición perfectamente ordenada.

Por ejemplo: consideremos las siguientes tablas: 

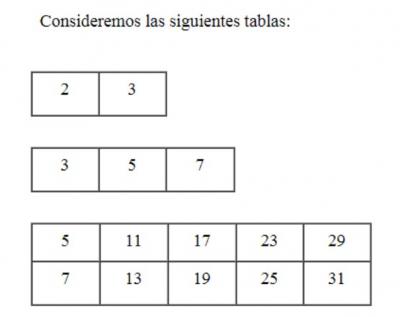
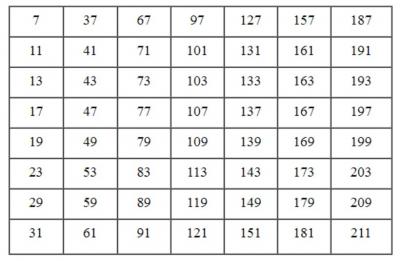
Denominemos las tablas según el primer número que aparece en cada una de ellas. La tabla del 2 está compuesta por 2 columnas, la tabla del 3 se compone, a su vez, de 3 columnas, la del 5 se compone de 5 columnas y la del 7 se compone de 7 columnas.

Puede observarse también que cada renglón en las tablas contiene una serie de números que, a partir de la primera columna, se van incrementando en forma constante hasta el final del renglón. Así, en la tabla del 7, el incremento es 30, pues, a partir del 11, por ejemplo, cada columna contiene un número igual a la columna anterior más 30.

En una tabla, el incremento para las columnas es el mismo en toda ella. Por ejemplo, en la tabla del 2, el incremento es 1, en la tabla del 3 el incremento es 2, en la del 5 el incremento es 6 y en la del 7 el incremento es 30. 

El incremento de cada tabla, excepto la primera, es igual a la multiplicación de los primeros números de las tablas anteriores. Así, lo que se incrementa en la tabla del 7, es igual a 5 • 3 • 2, es decir, 30; mientras que en la tabla del 5 es igual a 3 • 2, es decir 6, y en la tabla del 3 el incremento es 2.

Debe notarse que la primera columna de cada tabla incluye los números de la tabla anterior, excepto el primero y sus múltiplos, y que, además, el primer múltiplo del número con que se inicia cada tabla es el cuadrado de dicho número. Por ejemplo, en la tabla del 7, la primera columna la forman los números de la tabla del 5, excepto el mismo 5 y el 25, y el primer múltiplo de 7 que aparece es el 49. En cada renglón solamente aparece un múltiplo del primer número de la tabla.

Ahora bien, la mayoría de los números de las tablas son primos, pero seguramente son primos los que aparecen entre el primer número y su cuadrado. Es claro que, entre otros, no son primos los múltiplos del primer número (uno en cada renglón).

Dado que cada tabla se construye de la misma manera a partir de la tabla anterior, es posible entonces generar los números primos indefinidamente y construir las tablas del 11, 13, 17, etc., aunque por ahora sólo hemos puesto hasta la tabla del 7. 

Principio básico
Los números primos forman grupos que se incluyen en conjuntos de números que pertenecen, dentro de un cierto rango, al valor de y en la ecuación de una recta, y = mx + b, cuya pendiente es igual al producto de la multiplicación en serie de los números primos hasta uno determinado, m = P1 • P2• P3 ... • Pn, y cuya constante, b, está dada por los valores de una ecuación análoga (Es claro que trabajamos considerando solamente los valores enteros).

Por ejemplo, los números 5, 11, 17, 23 y 29, pertenecen, dentro del rango que va de x = 0hasta x = 4, a la ecuación y = 6x + 5, en la que la pendiente es igual al producto de los números primos hasta el 3, es decir 2 • 3; mientras que la constante proviene de la ecuación y = 2x + 3, cuando x = 1.

Relación entre ecuaciones
Como se ve por el hecho de que la primera columna de cada tabla depende de los números de la tabla anterior, las ecuaciones de las rectas en las que se encuentran los valores primos para y, se relacionan entre sí porque la constante b de una ecuación dada se asigna de acuerdo a los valores de y en la ecuación análoga en la cual la pendiente es igual al producto de la multiplicación de los números primos hasta el número primo anterior al de la multiplicación para obtener la pendiente de la ecuación dada. 

Por ejemplo, en la ecuación y = 6x + 5, la constante proviene de la ecuación y = 2x + 3, cuya pendiente viene dada solamente por el 2, es decir, el “producto” hasta ese punto de la multiplicación en serie de los números primos, que es “anterior” al producto P1 • P2. Los valores de y en y = 2x + 3, dentro del rango adecuado, son la constante de y = 6x + 5 y de y = 6x + 7.

El rango de los valores de x a tener en cuenta en una ecuación viene determinado en su valor máximo, por el siguiente número primo de la serie de donde se obtiene la pendiente menos uno. El valor mínimo es cero.

Por ejemplo, para y = 6x + 5, el mínimo para x es cero y el máximo 5 – 1, pues P1 • P2 es igual a 2 • 3, y el siguiente número primo es 5. En este caso, para x = 0, tenemos y = 5; para x = 1, y =11; para x = 2, y = 17; para x = 3, tenemos y = 23; y para el valor x = 4, tenemos y = 29. Los valores de y incluyen un conjunto de números primos (en este caso todos los valores en este rango son primos, pero no necesariamente ocurre así en otros casos).

La primera ecuación que sirve para iniciar la serie de ecuaciones que, según lo explicado, están relacionadas entre sí, es y = x + 2, donde el rango de x va de cero a uno.

Condiciones

Los números del conjunto de valores de y de una de estas ecuaciones son primos si son menores que el cuadrado del número primo, Pn, que sirvió de referencia para determinar el valor máximo de x.

Retornando a las tablas

Señalando cuanto dicho en las tablas propuestas tenemos:

Tabla del 2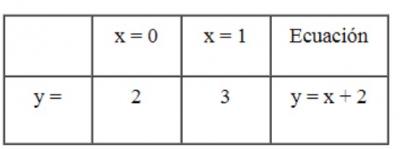

De donde P1 = 2 y P2 = 3, ya que 2 y 3 son menores que el cuadrado de P1.

Tabla del 3

De donde P3 = 5 y P4 = 7, menores que el cuadrado de P2.

Tabla del 5

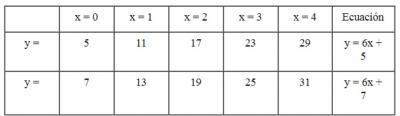
De donde P5 = 11 , P6 = 13, P7 = 17, P8 = 19 , P9 = 23, menores que el cuadrado de P3 

Tabla del 7

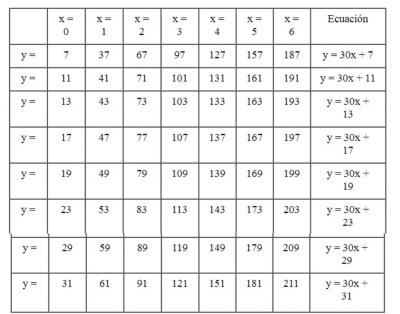
De donde P10 = 29 , P11 = 31, P12 = 37, P13 = 41 , P14 = 43, P15 = 47 , menores que el cuadrado de P4.

Si se desea abreviar para saber cuáles son primos de los restantes números de la tabla del 7, por ejemplo, se podría aplicar a ellos un método como el de la Criba de Eratóstenenes, método muy sencillo y rápido de aplicar, que podrías conocer más claramente y de que manera se puede aplicar visitando la siguiente url https://wikimat.es/numeros/primos-compuestos/ y donde ademas podras entender un poco mas acerca de los números primos.

También podrías verificar si son múltiplos o no de los números de la tabla mayores del mismo 7. Por ejemplo, 107 no sería primo si fuera múltiplo de 11 (no es múltiplo de 7, pues solamente hay uno en cada renglón, y en su renglón está el 77); pero no es múltiplo de 11, ya que el primer múltiplo de 11 en la tabla es el 121, luego, 107 es primo.